Hernán Santiago Nottoli
Arquitecto – Doctor en Arquitectura
Universidad de Buenos Aires
Creador y Codirector del Centro de Matemática y Diseño
Facultad de Arquitectura, Diseño y Urbanismo (UBA)
Hoy existen nuevos conceptos que se han gestado en los últimos tiempos y entre los renovadores campos matemáticos que se usan al diseñar se destaca: la geometría fractal. En este trabajo se pretende incursionar en esa rama del conocimiento, acompañando las ideas centrales con ejemplos de diseño de reconocido valor en el campo internacional. El objetivo central es mostrar una herramienta que posibilita enriquecer el proceso interviniente y la metodología se apoya en destacar los pasos sucesivos a seguir para aplicar estas novedosas ideas en el campo proyectual. Aunque muchos personajes dedicados a la creación de obras artísticas, de orden arquitectónico y urbanístico no suelen ser amigos de la matemática, hoy en día puede afirmarse que esa disciplina es un aliado imponderable en el proceso de diseñar. El colofón del trabajo destaca las válidas conclusiones que se espera que sean argumentos legítimospara defender las ideas centrales de esta presentación.
Today there are new concepts that have been created in recent times and among the innovative mathematical fields that are used when designing, one of them is the fractal geometry. This work aims to venture into that branch of knowledge, accompanying the central ideas with design examples of recognized value in international fields. The central objective is to show a tool that makes possible to enrich the intervening process, and the methodology is based on highlighting the successive steps to follow to apply these novel ideas in the design field. Although many people dedicated to the creation of artistic, architectural and urban works are not usually friends of mathematics, today it can be said that this discipline is an imponderable ally in the design process. The culmination of the work highlights the valid conclusions that are expected to be legitimatearguments to defend the central ideas of this presentation.
PALABRAS CLAVE: Arquitectura Geometría Fractal Modelos Ejemplos
KEYWORDS: Architecture Fractal Geometry Models Examples Architecture
FECHA DE RECEPCIÓN: 29/04/2024 | FECHA DE ACEPTACIÓN: 25/05/2024
DOI: https://doi.org/10.30972/arq.237660
Acaso no se recurre a una herramienta como la matemática en programas computacionales, imágenes digitalizadas, musicalizaciones, incluso con instrumentaciones de base numérica (la lira, las flautas por citar un par, y otros instrumentos de la antigüedad tienen su fundamento formal y sonoro en series matemáticas). etc. La arquitectura de vanguardia ya no puede escaparse hoy día de las más variadas geometrías que son fuente de inspiración de sus diseñadores. Lo mismo sucede con aquellos que forman parte de los objetos cotidianos de uso del hombre moderno, desde los automóviles hasta los artefactos que se encuentran en cualquier hogar.Y no acaba ahí la utilidad de las formas y las creaciones que además recurren a programas de base numérica y son de uso habitual en vestimentas, calzados, estampados y máquinas automáticas de confección de prendas varias. Pero esa milenaria disciplina que es la matemática ha desarrollado en la historia una amplia variedad de ramas que se han ido enriqueciendo a lo largo de los tiempos.
En este trabajo querríamos dedicarle unas líneas a una rama que puede considerarse de las más modernas, si se tiene en cuenta que nació y se desarrolló a finales del Siglo XX, muy poco tiempo para la “historia de los números”. Y en todo este artículo se han considerado conceptos que se pueden consultar con mayor detalle y extensión en los libros: Perera J, Perera J.(h) y Spinadel V. (1993). “Geometría Fractal”. Nueva Librería. Y en Spinadel V. (1995) “Orden y caos: el borde fractal”, Anales de la Sociedad Científica Argentina, Buenos Aires, vol. 225, No. 2, 129-141, mencionados en la Bibliografía.
Vamos a hablar en los siguientes párrafos del tema de los fractales, analizando a continuación sus características generales más significativas. La geometría fractal es fundamentalmente un nuevo lenguaje matemático. Explicando en forma sencilla qué es un fractal, puede decirse que la palabra fractal viene del vocablo latino fractus, que significa interrumpido o irregular.
Este nombre fue introducido en la década 1970 – 1980, por el matemático Benoit Mandelbrot, quien basándose en trabajos anteriores de su colega, el catalán Gaston Julia y con la ayuda de gráficos computarizados en el centro IBM de Nueva York, elaboró sus investigaciones, que han sido fuente de esta nueva matemática, generadora de formas a partir de un modelo algorítmico.
Una de las propiedades características de un fractal es su invariabilidad ante los cambios de escala. Fue el primero en estudiar el tema y en explicar cómo a partir de cualquier función compleja se puede fabricar, por medio de una sucesión definida, un conjunto cuya frontera es imposible de dibujar a pulso por ser de longitud infinita, entre otras propiedades. Esta propiedad de autosemejanza se presenta de muy diferentes maneras: algunos casos de autosemejanza son matemáticamente exactos, mientras que otros casos, que son los que se pueden hallar en el mundo real, son sólo aproximadamente autosemejantes. Si se analiza en primer lugar ese lenguaje desde un punto de vista estrictamente matemático, se verá que estas entidades constituyen un nuevo tipo de geometría. Mientras que los elementos de la geometría llamada euclidiana son líneas, planos, círculos, etc. los elementos de la geometría fractal son algoritmos que pueden ser traducidos en forma de estructuras. Evidentemente, Mandelbrot creó una disciplina, que tanto puede ser tomada desde un punto de vista riguroso, con sus implicancias de matemática sofisticada y de alto nivel, como puede ser accesible para la gente que no quiere oír sobre números. Vivimos en un mundo donde la geometría fractal se presenta de las más variadas formas, que no son más que sucesiones de imágenes que van surgiendo del conjunto de Mandelbrot y donde basta con dar una clave para indicar cómo cada imagen se deriva de otra previa. Por citar un mecanismo de fácil comprensión, vale mencionar cómo en una computadora es factible calcular un valor numérico para cada punto sobre la pantalla y a continuación asignar un color al número (p.ej. todos los puntos con un valor de tres son rosados, todos los puntos con un valor de cuatro son rojos, etc).
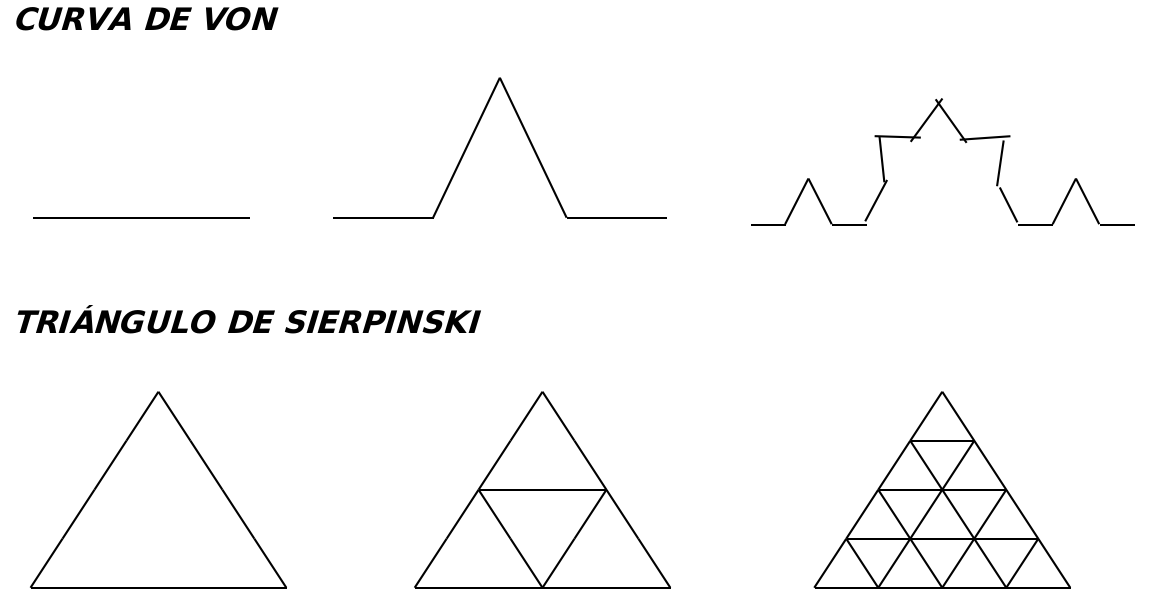
A partir de allí las imágenes que se pueden generar con la ayuda de otros programas de mayor complejidad son casi infinitas y dan paso a la creatividad en su más amplia expresión en campos del arte, como de mecanismos lúdicos o de aplicación en áreas tan disímiles como la industria o el diseño. Los siguientes son algunos ejemplos clásicos de subdivisión de un elemento geométrico según el criterio fractal (figuras 1). Ejemplos extraídos del libro “Enseñanza de matemática para arquitectos y diseñadores” cuyo autor es el mismo del presente artículo. Es factible observar en ellos que el mecanismo aplicado en el primer paso se reitera en los sucesivos (p.ej. dividir en 3 partes el segmento original y sustituir la parte central por dos segmentos de igual módulo que los laterales y que se unen cuspidalmente, o a partir de un triángulo equilátero, inscribir uno menor en su interior cuyos vértices se apoyen en el punto medio de los lados de el o los triángulos resultantes del paso anterior

Figura 1. Modelos fractales, dibujo en Word generado por el autor
Más novedoso y relacionado con el teorema de Pitágoras es el modelo fractal llamado “árbol pitagórico” (figuras 2).A partir de un triángulo rectángulo, se grafican las áreas cuadradas que se corresponden con las gráficas del cuadrado de la hipotenusa (C) y los cuadrados de los catetos (A, y B) donde se cumple la conocida fórmula pitagórica: A2 + B2 = C2
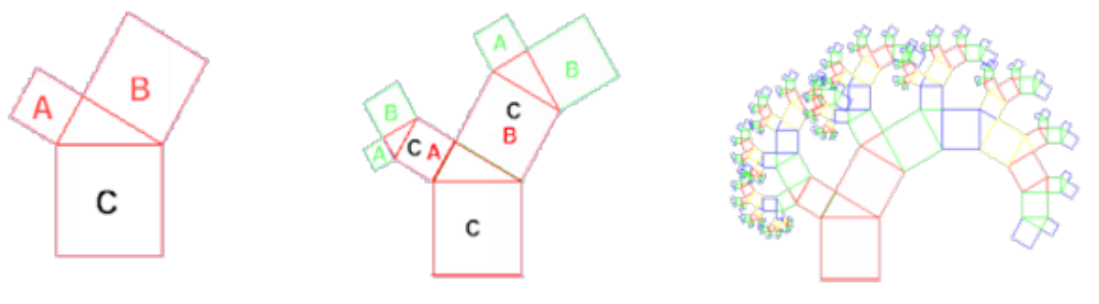
Figura 2. Modelos fractales, dibujo en Word generado por el autor
Y luego, generando nuevos triángulos rectángulos y tomando como medida de la hipotenusa de ellos los lados de los anteriores cuadrados A y B volver a graficar la relación pitagórica en sucesivos pasos.Es interesante destacar en este último ejemplo, que en cada iteración, la suma de los cuadrados que se agregan es igual al área del cuadrado C original, lo cual es fácilmente demostrable aplicando el teorema pitagórico. Y la paradoja es que si se repitiera indefinidamente el proceso, la superficie resultante debería ser infinitamente grande y sin embargo su gráfica no excedería el tamaño de un sector de esta página.Una parte de la fascinación de este tipo de matemáticas es el espectáculo de la simplicidad que redunda en complejidad, mediante la repetición simple de una forma propia. Otra parte son las formas asombrosas que se pueden lograr con algoritmos más sofisticados (ver figura 3) generada por el matemático Javier Barrallo, miembro del Departamento de Matemática. Ejemplo extraído del libro “Topología aplicaciones a la arquitectura y el diseño” cuyo autor es el mismo del presente artículo.
Y también la idea es que esta geometría puede explicar procesos de cómo opera la naturaleza y consecuentemente el diseño de gran parte de sus maravillas naturales (ver figuras 4) que no responden a geometrías rigurosas de figuras o cuerpos definidos por fórmulas estrictas – es decir las surgidas de la geometría euclideana – sino por secuencias de orden fractal.
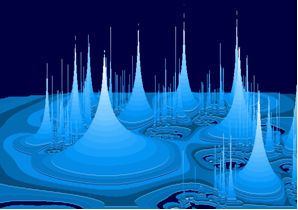
Figura 3. Generada por el matemático Javier Barrallo, miembro del Departamento de Matemática Aplicada en la Escuela Técnica Superior de Arquitectura de la Universidad del país Vasco - Euskal Herriko Unibertsitatea Aplicada en la Escuela Técnica Superior de Arquitectura de la Universidad del país Vasco - EuskalHerriko Unibertsitatea e integrante del Centro de Matemática y Diseño de la Universidad de Buenos Aires

Figura 4. Estructuras fractales. Origen es.m.wikipedia.org. All may be freely used (libre disponibilidad
Pueden aparecer toda clase de formas de apariencia orgánica: una rama, una hoja, una flor, un caracol, etc. así como visiones de la cambiante naturaleza tales como las nubes o el agua en movimiento. A diferencia de la geometría euclidiana, la geometría fractal parece ser capaz de describir los tipos de formas que realmente ocurren en nuestro mundo orgánico.
Esta nueva geometría fractal también explica el crecimiento y desarrollo de ciertas implantaciones urbanas, sobre todo aquellas de generación no planificada o que responden a patrones o modelos condicionadas básicamente por aspectos topográficos del emplazamiento. Asimismo las condicionantes históricas de la aparición de una ciudad o núcleo urbano, son muchas veces de una causalidad aleatoria, que generan un ordenamiento de los elementos constitutivos de la morfología urbana que también responde a este modelo fractal.
Son numerosos los ejemplos de ciudades en el mundo que se han gestado siguiendo un modelo fractal, elegimos para este trabajo la Ciudad de Niza, en Francia, en primer lugar por haber tenido el placer de disfrutarla recorriendo sus calles, su arquitectura y sus vistas panorámicas en particular hacia el Mar Mediterráneo.
En todos los casos que se pueden observar esa característica analítica decrecimiento espontáneo y no planificado de una urbe, podríamos citar como los más determinantes los siguientes:
La falta de reglamentaciones urbanísticas en el momento de la implantación original
La topografía del lugar de emplazamiento y su entorno
Las condiciones socio económicas del lugar
Las tecnologías constructivas disponibles en las primeras épocas de las construcciones
La estructura de los suelos donde se asienten las cimentaciones de lo construido
La proximidad a otros países con los cuales puedan generarse hipótesis de conflictos territoriales o bélicos
Por supuesto que el listado anterior no es taxativo ni excluye condicionantes variados que asimismo influyen en los trazados urbanísticos. Podrían citarse los avances comerciales que devendrán en el futuro, las nuevas tecnologías constructivas que vayan surgiendo para construir, etcétera y más etcéteras que quizás no se puedan imaginar con los crecimientos acelerados que verifican hoy en las ciencias de la civilización
Lo cierto es que en el caso de Niza, el tejido urbano se gestó en sus inicios adaptándose a un terreno accidentado en pendiente hacia el mar y su casco antiguo nació como una especie de triángulo entre la colina del castillo que siempre ocupa lugar destacado, el mar y el río Pailón que corre por sus entrañas. Esta idea se tomó como leit motiv en el trabajo tirulado “Análisis de diseños de planeación según modelos fractales y topológicos", cuyo autor es asimismo el que presenta este artículo.
Con el tiempo se extendió primero hacia el este y el puerto, y más tarde hacia el norte y a partir del siglo XIX, la ciudad empezó a crecer a lo largo de la costa y hacia el interior. Actualmente la ciudad está claramente dividida en dos: la orilla izquierda del Pailón, más antigua, se caracteriza por un estilo urbano similar al de Torino, ciudad hermana itálica que fue habitada por el pueblo de los taurinos que le dieron el nombre.
La ciudad se desarrolló en el sigloI siguiendo el trazado de un campamento romano con tres o cuatro ejes horizontales principales que se cruzan con vías perpendiculares queson de menor importancia, podríamos también decir que conforman el clásico damero español que es posible observar como modelo en la mayor parte de la ciudad de Buenos Aires, capital de Argentina. La orilla derecha de Niza es más nueva y más afrancesada, ya que presenta un estilo mucho más haussmaniano, con diagonales que cruzan el entramado citadino al estilode París.
Pero pareció interesante para este trabajo mostrar un plano de Niza del año 1624 (ver figura 5) donde claramente surge la impronta fractal, y aunque no sea una particularidad que haga al análisis de este trabajo, considerando que el mismo está dirigido a profesionales del diseño, vale destacar una condición del sistema de representación de la época y es cómo la imagen muestra los edificios en escorzo y no como una vista aérea, ni como una vista perspectivada con puntos de fuga, técnicas que recién se crearán en detalle en Europa en los siglos XV y XVI pero que no llegaron para la graficación de este plano sino hasta el siglo XVII.
En cuanto al tema antes mencionado de las regulaciones gubernamentales que son altamente aconsejables que existan en los centros urbanos, es un dato a destacar que en 1832 se creó el Consejo de Ornamento (Consiglio d’Ornato en italiano que era el idioma oficial de la época) y que fue el que a partir de su creación se encargó de la organización estructural de Niza y de su evolución urbana. Surgieron en base a sus ordenanzas los grandes bulevares de circunvalación, que llevan los nombres de destacadas personalidades europeas, como el bulevar Victor Hugo; la avenida Jean Médecin y las plazas que aún existen y que fueron bautizadas como André Masséna y Giuseppe Garibaldi.
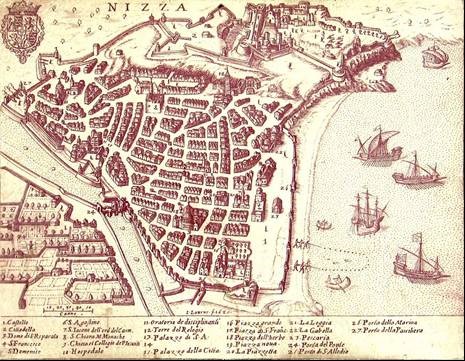
Figura 5. Niza en 1624. Origen: es.m.wikipedia.org. All may be freely used (libredis ponibilidad)
Hoy en día la ciudad vieja se conserva con la planificación de las ciudades italianas en la época moderna, pero las calles son estrechas y mantienen la sinuosidad que le impuso la morfología del terreno.Dos siglos de guerras que siguieron a los tiempos en que se graficó el plano previo, no alteraron demasiado los trazados urbanístico originales. Fue en ese entonces cuando finalmente la ciudad se convirtió en un dominio del Imperio Francés.
Y que otro interesante ejemplo arquitectónico se puede mencionar como original y creativo por la importancia y genialidad de quien lo generó en su momento. Nos referimos en primer lugar a su gestora que fue la prestigiosa arquitecta anglo-iraquí Zaha Hadid quien puede decirse que amplió las posibilidades formales y estructurales de la arquitectura y redefinió el concepto de fluidez espacial, y según ella misma expresó en más de una oportunidad, tuvo como disciplina inspiradora la geometría fractal para sus proyectos. En el Congreso de la UIA de Estambul, Turquía del año 2005 fue grato escuchar personalmente su conferencia sobre su obra arquitectónica y destacar que ella se basaba en su impronta heurística en la geometría fractal. A ese Congreso asistió con un colega el autor de este artículo según se menciona en la Bibliografía como Terranova A. y Nottoli H. (2005) donde cumplieron desarrollando tareas periodísticas para diversos medios locales, entre ellos la revista “Todoobras” dedicada a la arquitectura y el diseño. Es interesante mencionar que Hadid estudió matemáticas en la American University de Beirut antes de trasladarse a Londres en 1972. En la Architectural Association School, que es la escuela independiente de arquitectura más antigua en el Reino Unido, y una de las instituciones de diseño más prestigiosas fue donde se graduó como arquitecta en 1977. Fue la primera mujer en 2004 que obtuvo el Premio Pritzke, el más importante galardón de la arquitectura. El ejemplo que se desea considerar a continuación y que convalida la afirmación es el Pabellón Puente fue uno de los edificios principales de la Expo 2008 de Zaragoza, diseñado por Hadid y que conecta la margen derecha del río Ebro con el recinto de la Expo. Su planta tiene forma de sostén de la flor gladiolo, como puede observarse en las siguientes figuras 6a y 6b. La vista aérea de ese enlace entre ambas márgenes muestra la similitud con el tallo de la flor antes citada, la cual como todo elemento de la naturaleza de formas no convencionales, solo puede explicarse geométricamente como fractal. El Pabellón Puente constituye un híbrido entre pasarela y pabellón expositivo, la imagen de gladiolo parte de la orilla con un único tallo, y se divide en su centro en tres “vainas” que desembarcan en la ribera opuesta. Para tener una idea de la complejidad del proyecto se muestra a continuación un corte (ver figura 7) de las instalaciones que componen el complejo edilicio.

Figura 6a. Vista aérea del Pabellón Puente

Figura 6b. Rama del gladiolo
Figuras6a y 6b. Fuente: ver Figura 7 con iguales datos
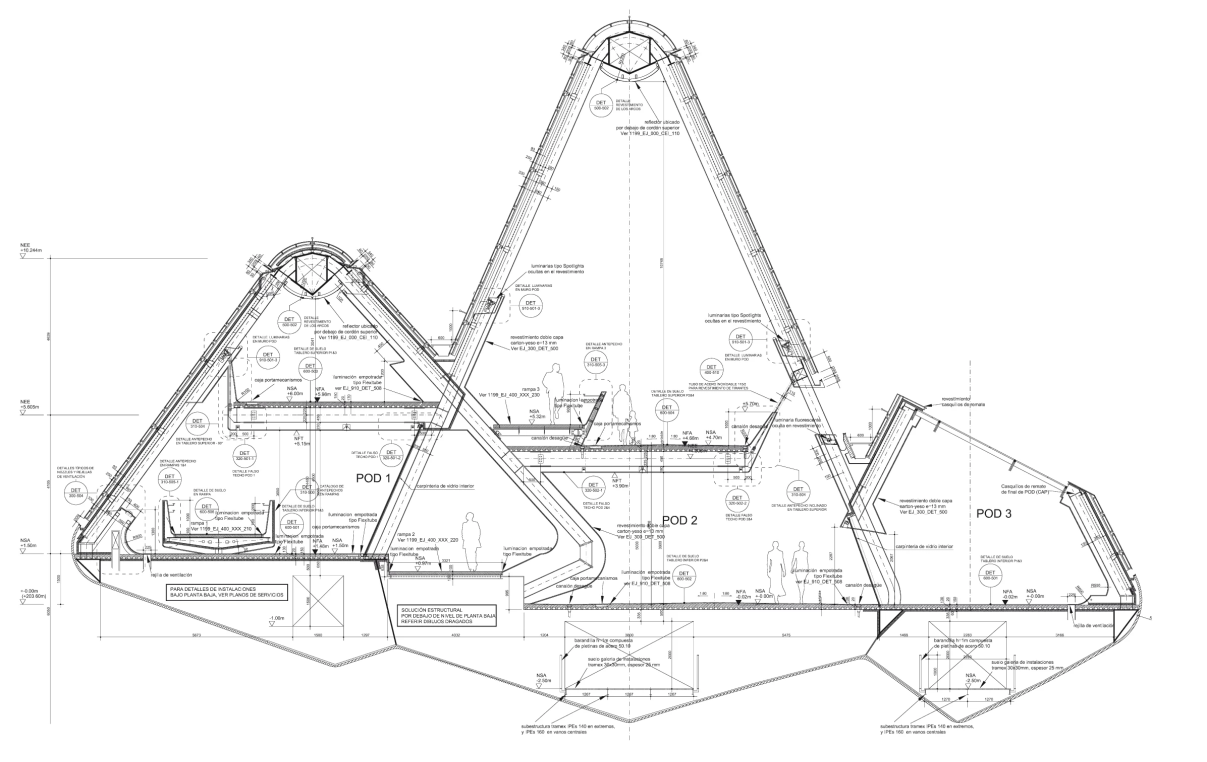
Figura 7. Fuente de la figura 7. Fue tomada de Arquitectura Viva S.L. Autorizado su uso por el sitio web según norma expresa: “El usuario se compromete a respetar los derechos de Propiedad Intelectual e Industrial titularidad de Arquitectura Viva S.L.Podrá visualizar los elementos del portal e incluso imprimirlos, copiarlos y almacenarlos en el disco duro de su ordenador o en cualquier otro soporte físicopara su uso personal”
El diseño, tal cual puede apreciarse en el gráfico de corte antes mostrado, se definió en forma de diamante – se asemeja a una pieza tallada de ese costoso y deslumbrante cristal – logrando con su morfología conformar una estructura espacial que optimiza la distribución de cargas, logrando que el espacio bajo el último forjado pueda ser resuelto con una viga cajón que alberga todas las instalaciones. Esta sección romboidal fluye extruida a lo largo de cuatro trayectos ligeramente curvados, generando cuatro elementos diferenciados, que se entrelazan siguiendo criterios precisos con el objetivo de reducir la dimensión de los elementos portantes y optimizar el sistema estructural. La envolvente o piel del proyecto se inspiró en diferentes superficies naturales, optando finalmente por la que su diseñadora consideró la solución más apropiada: unas escamas de tiburón, las cuales tanto por su aspecto como por su funcionamiento, se adaptan a las complejas curvaturas del diseño. Esta envolvente está generada mediante el solapamiento, a modo de escamas, de paneles prefabricados de FRC (Fiber Reinforced Composite), un hormigón reforzado con fibras que aumentan su integridad estructural. Los materiales de las fibras incluyen acero, vidrio, compuestos sintéticos y naturales. Ello también redunda en cierta libertad para distribuir los espacios interiores, que siguiendo los modelos fractales están concebidos como si hubieran sido modelados por la luz solar o vientos dominantes de la zona. Así también se concibieron las aberturas que permiten el ingreso de la luz solar, que si bien no son de gran magnitud, su multiplicidad y su ubicación en el nivel inferior de la pasarela las hacen más que suficientes. El Pabellón Puente se asienta sobre apoyos ejecutados con pilotes que fueron hincados hasta encontrar asentamientos sólidos que los sustentaran. La inestabilidad del subsuelo en torno al río, como toda zona próxima a vías acuáticas, obligó a que los pilotes buscaran base firme cerca de los 70 metros por debajo de la superficie, resultando entonces de los más profundos construidos hasta el momento en la península ibérica.
Si se analizaran los modelos matemáticos que rigieron fundamentalmente hasta ahora a la mayoría de los trazados urbanísticos proyectados antes de concretar la ejecución de los emplazamientos, es dable señalar que nos encontraríamos con ramas matemáticas como la geometría euclideana y alguna rama de la topología. Tal es el caso de dos de los proyectos concretados en nuestra América del Sur. El primero una ciudad no muy conocida en el mundo, pero que posee el mérito de haber sido la primera en nacer sobre un papel para luego erigirse en la ciudad Capital de la Provincia de Buenos Aires, Argentina. Se trata de La Plata (ver figura 8),fundada por el Gobernador Dardo Rocha en 1882 como resultado de un proyecto que este político encargara al Departamento de Ingenieros del Gobierno local, que funcionaba bajo la Dirección del profesional Pedro Benoit. Resultó ser la primera de esta especialidad en el continente americano. Su casco histórico inicial se conformó como un cuadrado perfecto, en el cual calles y avenidas se cruzan a 90º y la trama urbana está seccionada por avenidas ubicadas en diagonal a 45º respecto del cuadrado envolvente. En este caso los recorridos de punto a punto ida y vuelta pueden variarse, pero inevitablemente resultan de igual longitud cualquiera sea la opción de menor traslado que se elija. El segundo ejemplo demostrativo de la realidad que se menciona en estas conclusiones es la conocida y destacada urbanísticamente Capital de Brasil (ver figura 9), denominada Brasilia, nacida en 1960 como resultado del talento de Lucio Costa como principal urbanista y de Oscar Niemeyer como el genio arquitectónico que la dotó de verdaderas joyas del diseño. Su trazado en esta ocasión se gestó pergeñando una morfología en planta según un modelo arbóreo, donde la avenida principal es el tronco del cual emergen las vías secundarias como ramas del árbol respetando todo una simetría axial. En Brasilia, además de la magnitud manifiesta que debe recorrerse a pié entre edificios o por espacios abiertos, cualquier trayecto entre dos puntos de la ciudad ida y vuelta no posibilita más que un único recorrido óptimo que no implique salir de la distancia mínima a transitar. Si se comparan ambos ejemplos con el trazado de la ciudad de Niza antes mencionada como ejemplo de modelo fractal urbanístico (ver la previa figura 5) y tantas otras que poseen esa cualidad, se defiende la idea de que esta última herramienta matemática y que rige este trabajo, es poseedor de una riqueza formal que permite: recorridos con mayores posibilidades óptimas en distancias de un punto a otro de la trama, ángulos de visión del entorno más ricos en variedad, multiplicidad de implantaciones según los puntos cardinales que hacen a la iluminación natural y en algunos casos a vientos dominantes. En resumen un modelo más versátil con el cual imaginar heurísticamente el trazado de una urbe.

Figura 8. Planta de la ciudad de La Plata. Fuente www.google.com
Figura 9. Planta de la ciudad de Brasilia. Fuente: www.google.com
Por ello se cierra este trabajo de ver la geometría fractal como poseedora de conceptos y modelos con características que no se refieran tan solo a magnitudes en las que intervengan valores numéricos, sino por el contrario, a propiedades de orden topológico, donde se enfatizaron las relaciones entre elementos vinculados al diseño, con ejemplos en los que se ha buscado presentar la temática con un enfoque más novedoso y conceptual. Una herramienta más para planificar proyectos urbanísticos o de orden general en arquitectura.
Nottoli H. (2017). “Enseñanza de matemática para arquitectos y diseñadores”. Ediciones Diseño Editorial. ISBN 978-987-4000-88-0.
Nottoli H. (2021). “Topología aplicaciones a la arquitectura y el diseño”. Diseño Editorial, ISBN 978-64360-508-1.
Nottoli H. (2021). "Análisis de diseños de planeación según modelos fractales y topológicos". Trabajo de investigación. XV Congreso de la Asociación Latinoamericana de Escuelas de Urbanismo y Planificación (on line).
Perera J. y Perera J.(h) y Spinadel V. (1993). “Geometría Fractal”. Nueva Librería.
Spinadel V. (1995) “Orden y caos: el borde fractal”, Anales de la Sociedad Científica Argentina, Buenos Aires, vol. 225, No. 2, 129-141,
Spinadel V. y Nottoli H. (2005). “Herramientas Matemáticas para la Arquitectura y el Diseño”, Ediciones FADU. ISBN 950-29-0833-3.
Terranova A. y Nottoli H. (2005). Asistentes al XX Congreso de la Unión Internacional de Arquitectos (UIA). Tareas periodísticas. Disertó en esa ocasión entre otros grandes maestros, la Arqta. Zaha Hadid.
web: https://fog.ccsf.edu (citada en varias imágenes)